Intrinsic equation

In geometry, an intrinsic equation of a curve is an equation that defines the curve using a relation between the curve's intrinsic properties, that is, properties that do not depend on the location and possibly the orientation of the curve. Therefore an intrinsic equation defines the shape of the curve without specifying its position relative to an arbitrarily defined coordinate system.

The intrinsic quantities used most often are arc length $s$ , tangential angle $\theta$ , curvature $\kappa$ or radius of curvature, and, for 3-dimensional curves, torsion $\tau$ . Specifically:

The natural equation is the curve given by its curvature and torsion.
The Whewell equation is obtained as a relation between arc length and tangential angle.
The Cesàro equation is obtained as a relation between arc length and curvature.

The equation of a circle (including a line) for example is given by the equation $\kappa(s)=Cte$ where $s$ is the arc length and $\kappa$ the curvature.

These coordinates greatly simpilfy some physical problem. For elastic rods for example, the potential energy is given by

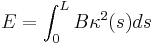
$E= \int_0^L B \kappa^2(s)ds$

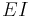where $B$ is the bending modulus $EI$ . Moreover, as 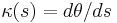$\kappa(s) = d\theta/ds$ , elasticity of rods can be given a simple variational form.

References

R.C. Yates (1952). A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards. pp. 123–126.
J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 1–5. ISBN 0-486-60288-5.

External links

Weisstein, Eric W., "Intrinsic Equation" from MathWorld.